十亿级数据过滤算法伪像——布隆过滤器布隆过滤器之前,先让我们看看这个业务场景

public class BloomFilterTest {   public static void main(String[] args){     int size = 1000000;     //布隆过滤器     BloomFilter bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, 0.001);          for (int i = 0; i < size; i++) {             bloomFilter.put(i);         }          List list = new ArrayList(1000);         for (int i = size + 1; i < size + 10000; i++) {             if (bloomFilter.mightContain(i)) {                 list.add(i);             }         }         System.out.println("误判数量：" + list.size());   } }

已经有很多开源框架帮我们实现了布隆管理器，比如 Google 出品的 Guava 工具库，其中就有开箱即用的布隆过滤器;

04.Guava 中的 BloomFilter

/** * 判断元素是否在布隆过滤器中 * @param value * @return */ public boolean contains(String value) {   if (value == null) {       return false;   }    for (HashFunction f : functions) {     if(!bitset.get(f.hash(value))){       //一个位置上不为1（true），就证明不存在，直接返回false       return false;     }   }    return true; }

判断元素是否在布隆管理器中，需要对入参进行 6 次 hash 运算，再查看结果对应的位置上是 0 还是 1(true or false)，如果其中一位是 0，表示数据肯定不存在，如果都是 1，表示数据(大概率)可能存在。

/** * 添加一个元素，得到hash运算后的结果，将对应的位置修改成1（true） * @param value */ public void add(String value) {   if (value != null) {       for (HashFunction f : functions) {     bitset.set(f.hash(value), true);       }   } }

增加元素的时候，对入参进行 6 次 hash 运算，并将结果对应的位置修改成 1(BitSet 对应的位置修改成 true)：

/** * 初始化 */ public BloomFilter() {   bitset = new BitSet(DEFAULT_SIZE);    for (int i = 0; i < seeds.length; i++) {       functions[i] = new HashFunction(DEFAULT_SIZE, seeds[i]);   } }

在构造函数中进行初始化，设置 BitSet 的长度，生成映射函数：

//定义一个质数数组，长度为6，可以生成6个hash函数，用于随机映射 private int[] seeds = {3, 7, 13, 31, 37, 61};  private HashFunction[] functions = new HashFunction[seeds.length];

我们还需要一组映射函数，这里可以使用加法 hash 函数，设置 6 个质数，对应 6 个不同的 hash 函数：

//设置一个布隆过滤器 private int DEFAULT_SIZE = 1 << 30;  private BitSet bitset ;

首先我们需要定义一个 bitmap，在 JDK 中，已经有对应实现的数据结构类
java.util.BitSet：

Code 不是目的，Coding 的过程是为了加深理解。

03.手写一个布隆过滤器

回到本文开头的那个业务场景，为了防止缓存穿透，可以使用布隆过滤器过滤掉肯定不存在的数据，误判的请求虽然还是会放到到数据库，但已经极大地减少了穿透的数量。

在存储空间和插入查询的时间复杂度都有巨大优势。

可以添加元素，但是不能删除元素(除非增加计数器);

二进制向量越长，映射函数越多，误判率越低;如果提前可以确定误判率，也可以反推出来布隆过滤器的长度;

可以确定一个元素肯定不存在，但是不能确定一个元素肯定存在;

02.特点总结

而且因为多个数据经过运算后可能会映射到同一个位置(138 和 189 的运算结果都有 12)，所以布隆过滤器很难做到删除，除非要为每一位增加一个计数器，删除的时候需要给计数器减 1，直到计数器为 0 时，才将布隆过滤器对应位置修改成 0。

对 13700000000 分别进行 hash1()、hash2()、hash3() 运算，得到三个结果 1、9、13，然后去判断第 1、9、13 位上的值是 0 还是 1，如果不全是 1 的话，就说明 13700000000 不在这个布隆过滤器上;这就确定了“某项数据肯定不存在”。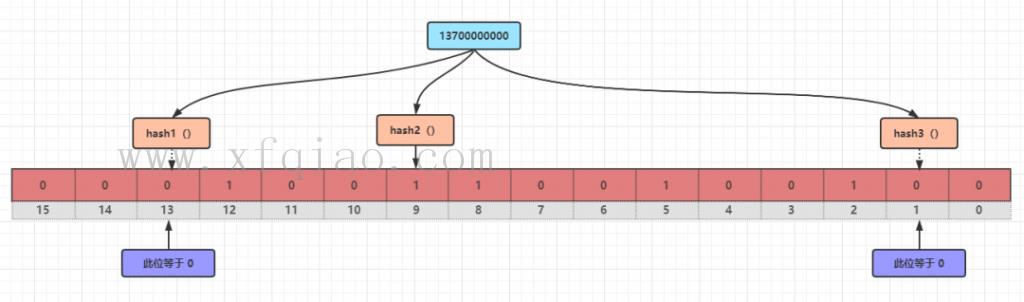

当然我们也可以看出来布隆过滤器有个问题，那就是不能保证数据肯定存在，比如对 18000000000 分别进行 hash1()、hash2()、hash3() 运算，得到的结果是 5、8、9，恰好这三位都是 1，但实际上这条数据并不存在，所以布隆过滤器有一定的误判率;

对 13800000000 分别进行 hash1()、hash2()、hash3() 运算，得到三个结果 5、9、12，把对应位置设置成 1;

对 18900000000 分别进行 hash1()、hash2()、hash3() 运算，得到三个结果 2、8、12，把对应位置设置成 1，现在 2、5、8、9、12 都是 1，其余元素都是 0;

如果我们想要验证某个电话号码是否存在，需要怎么做呢?

布隆过滤器初始化都是 0;

比如要根据客户手机号做为条件查询客户信息，通常会把手机号码设置成缓存中的 Key，让我们设置一个长度为 16 的布隆过滤器。

布隆过滤器是一个叫“布隆”的人提出的，它本身是一个很长的二进制向量(想象成数组)和一系列随机映射函数(想象成多个 Hash 函数)，二进制向量中存放的不是0，就是1(在学习布隆过滤器之前，可以先了解 BitMap 算法，便于理解)。

01.布隆过滤器的概念

那么有没有什么办法解决这个问题呢?这就可以使用【布隆过滤器】了，它可以确定“某项数据肯定不存在”。

这种方式可以减少数据库的访问次数，但是“当缓存中没有，就查询数据库”，在高并发的环境中依然会有风险，比如 90% 的请求数据都不在缓存中，那么这些请求就都会落到数据库上，这就是缓存穿透。

Redis 是软件架构中常用的组件，最常见的用法是将热点数据缓存到 Redis 中，以减少数据库的压力;查询过程中最常见的用法是：查询 Redis，如果能查询到则直接返回，如果 Redis 中不存在则继续查询数据库。

在正式讲解布隆过滤器之前，先让我们看看这个业务场景：

Mr Li

37276